機能
汎用有限要素法連成解析ソフトAMPS -機能
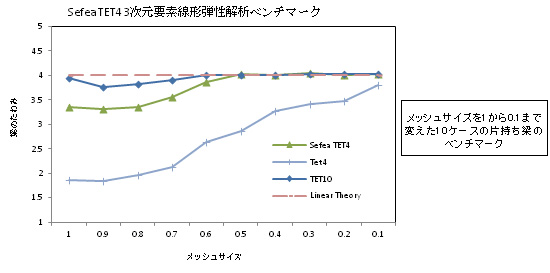
Sefea: エンリッチ有限要素テクノロジー搭載
Sefeaはメッシュレス法を応用した独自の数値計算技術により、1次要素の汎用性、低コストと2次要素に遜色のない解析精度、さらに安定性を実現しています。
- 接触、衝撃、非線形ひずみ解析、任意形状に対して自動分割で作成されたメッシュに対しても許容度が高く、ユーザー様が担当される現実の問題(異種材料や非線形解析など)の解析に対応しています。
- Sefeaには4節点テトラ1次要素(Sefea TET4)、3節点3角形1次要素(Sefea TRI3)、4節点4辺形1次要素(Sefea QUAD4)、3節点シェル1次要素(Sefea Shell3), 4節点シェル1次要素(Sefea Shell4)などを装備しています。
- マルチフィジクスの各物理場の定式化に統一されたSefeaのアルゴリズムは、応力/熱/流体/電磁場の各定式化の完全な連成を実現しています。
応力解析/衝撃解析
機械や構造物を設計する場合には、各部材の構成する材料の強さ、こわさ及び部材の安定性を十分に考慮して部材の形状や寸法を合理的に選定する必要があります。
AMPSを使用することによって、構造をモデル化することにより、荷重が作用する際の構造内の応力集中を解析することができます。
最近では、電気機器パッケージの対衝撃性が問題となっており、AMPSでは、陽解法と陰解法を使用することで衝撃予測シミュレーションを実現しています。
解析ライブラリ
AMPSでは、豊富な解析ライブラリを搭載しております。
ソルバーは、歪み増分法を使用して応力解析を実行します。
また、大変形を起こす座屈挙動に対しては、弧長法を使用して、飛び移り後の挙動を解析します。
ソルバーは、アダプティブ荷重増分コントロールによる陰的積分法が提供されています。
そして、ユーザは、微小変形則と有限変形則のいずれかの定式化を選択することができます。
- 静的応力解析/変位解析
静的問題に対して、変位、応力解析をおこなうことができます。 - 動的応力/変位解析
動的問題に対して、後退オイラー法による直接陰的時間積分を行うことで、変位、応力解析をおこなうことができます。
もう一つは、中央差分法による直接陽的時間積分を行うことで、連立方程式を解かずに変位、応力解析を高速演算におこなうこともできます。 - 非定常クリープ応答解析
クリープ挙動に対して、陽的時間積分法と陰的時間積分法を使用して、変位、応力解析をおこなうことができます。 - 固有振動解析
任意の段階で予荷重の効果を考慮して系の固有振動数を抽出することが可能です。 - 線形/非線形座屈解析
座屈挙動に対して、Riks法とCrisfiled法を使用して、座屈後の飛び移り挙動を解析することができます。
材料ライブラリ
AMPSでは、多くの材料モデルが用意されています。
すべての材料パラメータは、温度や任意の物理量変数への依存性を考慮することができます。
- 等方性弾性材料
等方性弾性材料は、弾性変形挙動を示す材料になります。
弾性挙動は、荷重を取り除くと元の形状(原形)に戻る材料になります。
AMPSでは、微小変形内における金属材料、樹脂材料、セラミック材料、コンクリート材料など。
また、シリコン材料、ガラス材料などの直交異方性や完全異方性を取り扱うことができます。 - 弾塑性材料
弾塑性材料は、生じる応力が小さい範囲内では材料は弾性的な挙動を示し、そして、応力がある限界を越えると変形は完全に元へもどらず、永久歪みが残るような挙動を示す材料になります。
AMPSでは、金属材料、樹脂材料の塑性変形を取り扱うことができます。
AMPSの塑性挙動モデルとして、Misesの等方性降伏条件が用意されており、等方硬化則を用いることができます。
さらに、繰り返し載荷に対しては、線形の移動硬化則と非線形の等方/移動硬化が用意されています。
また、砂などの粒状材料のためのMohr-Coulombの降伏条件も用意されています。 - 超弾性材料
超弾性モデルは、ゴムなどの材料に対する大歪みの弾性応答解析に用いられます。
AMPSでは、Mooney Rivlin構成式を仮定していますので9つのひずみ定数を指定することで超弾性材料を取り扱うことができます。 - クリープ材料
クリープ材料は、物体に力が加わった場合に時間とともに変形が進行する挙動を示します。
高温における金属材料にその典型的な例が見られます。
AMPSでは、ユーザサブルーチンを用意しているので複雑なクリープ式を定義することができます。
また、塑性モデルとあわせて取り扱うことができます。 - 圧電素子材料
圧電素子材料は、歪みが加えられると表面に電荷が現れ、電界が与えられると内部に応力が発生します。
AMPSでは、水晶などの圧電結晶体、圧電セラミックなどを取り扱うことができます。 - 初期応力の考慮
AMPSでは、材料に対して、初期応力を考慮することができます。 - ユーザ定義材料
ユーザサブルーチン機能(API)によって新しい材料モデルを取り扱うことができます。 独自の弾塑性モデル、クリープモデルなどを取り扱うことができます。
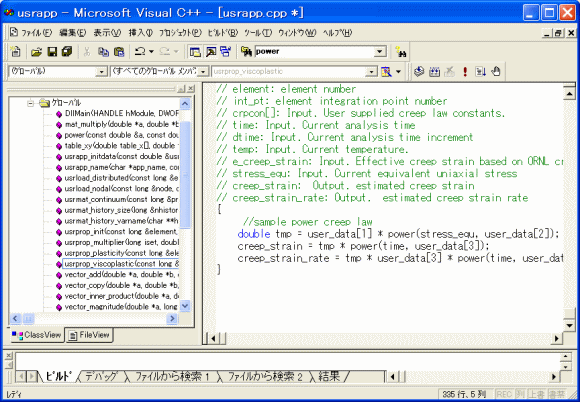
(クリープ歪み関数のユーザサブルーチン)
大変形解析
微小変形弾性論では表記できない現象(大変形)、たとえば、大歪み、大回転のような現象に対しては、AMPSでは、次の2つの手法を使用することができます。
- トータルラグランジュ法
この手法は、大変形であるが微小歪みの挙動を示す場合に使用します。 - アップデートラグランジュ法
この手法は、回転角が大きくて曲率表現内の非線形項が無視できないようなシェル構造や梁構造の応力解析/変位解析に使用します。
あるいは、塑性挙動を微小変形とみなすことができず、ネッキングを引き起こすような大歪みなどに使用します。
また、物体が座屈挙動を示す場合には、弧長法を使用することにより座屈後(飛び移り)の変形挙動を追跡することが可能です。
ラバーブーツの大変形シミュレーション
最近の機械や電気機器の製品開発において、ゴム材料を使用した機械部品が多くなっています。
たとえば、ラバーブーツの変形特性あるいはフィーリング特性を把握することは部品設計の中で非常に重要となります。
AMPSでは、このラバーブーツ変形挙動に対して、ムーニリブリン構成則を使用してゴム材料をモデル化することができ、さらに、アップデートラグランジュ法を使用して大変形(大回転)として取り扱うことができます。
下図は、直径50[mm]のラバーブーツに対して、30[mm]の強制変位を生じた際の変形の様子を示しています。
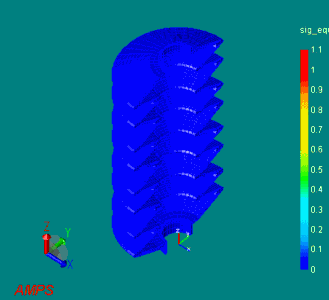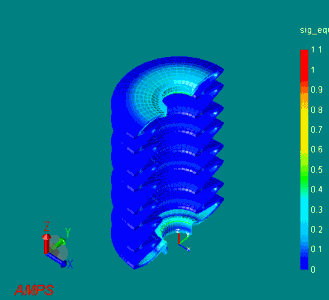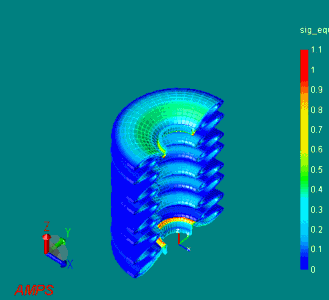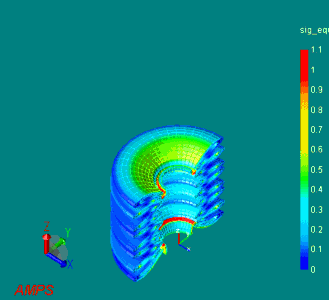
(ラバーブーツの大変形シミュレーション)
要素ライブラリ
AMPSでは、形状を自由にモデル化できるように、豊富な要素を搭載しています。
- 梁要素、トラス要素
- シェル要素
- 2次元平面歪要素、2次元平面応力要素、軸対称要素
- 3次元4面体要素、3次元5面体要素、3次元6面体要素
これらの要素は、線形要素から高次ラグランジュ要素への拡張が可能となっています。
また、微小変位だけではなく、有限歪みと有限変位に対して定式化されています。
数値積分には、完全積分、ガウス積分、Lobatto積分、選択低減積分を使用することができます。
伝熱解析
電子機器やパソコンなどの製品の開発時に直面する熱に起因する問題があります。
この場合、正確な製品の温度を把握する必要があります。
また、様々な工業分野では、高温領域で使用される機会が多くなってきています。
化学工業の分野では、反応効率を高めるために、高温化が促進され、1000℃以上の高温に固体がさらされることもめずらしくありません。
したがって、固体の温度分布を知ることは非常に重要になってきます。
AMPSを使用することにより、対流や輻射を考慮した製品の熱伝導解析を行うことができます。
解析ライブラリ
- 定常/非定常熱伝導解析
熱伝導問題に対して、定常状態、または、非定常状態を取り扱うことができます。 - 物性パラメータの温度依存性
熱伝導率、比熱、粘性抵抗に対する温度依存性を考慮することができます。
ヒートシンクの非定常温度シミュレーション
最近の電気機器の発達に伴い、回路等から発熱する熱問題が重要視されています。
発熱あるいは熱伝導により部品の温度が上昇すると性能が減衰する問題や熱変形による破壊が生じる場合もあります。
最近では、コンピュータや機械装置のCPUの発熱問題は重要な問題となっています。
このようなことから、ヒートシンクの設計において、ヒートシンクの温度状態を予測することは非常に重要になってきています。
AMPSでは、対流熱伝達あるいは輻射を考慮した非定常熱伝導解析を取り扱うことができます。
ここでは、50[mm]x50[mm]のフィン数8枚のヒートシンクに対して、時間変化による温度分布を表示しています。
また、フィンから空気への熱伝達は、平行平板と垂直平板の強制対流式により求められる熱伝達係数を定義しています。
したがって、空気速度、空気温度に依存した熱伝達係数を定義することができます。
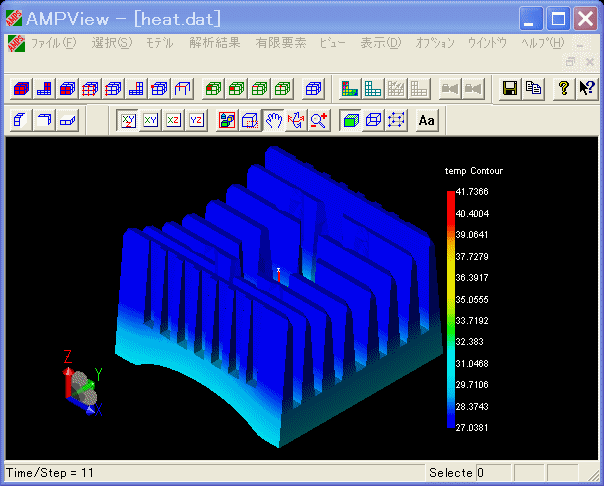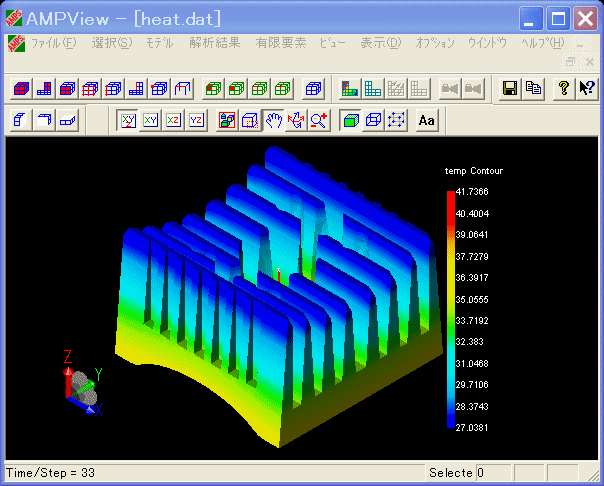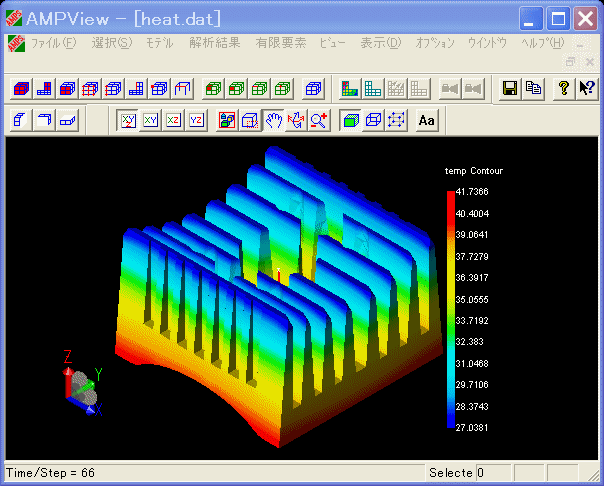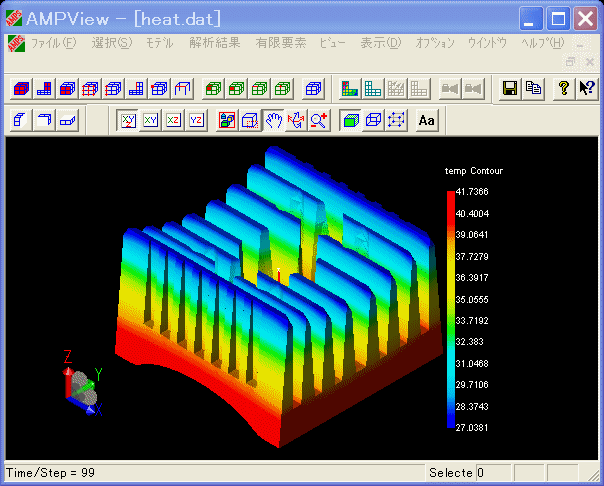
(ヒートシンクの温度シミュレーション)
連成解析手法
連成解析には、マトリクス連成とシーケンシャル連成の2つの方法があります。
マトリクス連成解析は、連立方程式を解く段階で連成が行われます。
したがって、複数の物理現象を1つのマトリクスで表現することが可能な手法となります。
線形の場合、最低1回のマトリクス計算で結果を得ることができ、また、解析が非常に早いです。
AMPSでは、ALE法を使用することにより、構造-流体-伝熱-電場のマトリクス連成解析が可能です。
一方、シーケンシャル連成解析は、複数の物理現象をそれぞれ単独に解析し、個々の解析で得られた結果を別の物理現象の解析に対して荷重として与える手法となります。
AMPSでは、OverSet法(重合格子法)を使用することにより、構造-流体-伝熱-電場のシーケンシャル連成解析が可能です。
ALE法
流れ場に、弾性構造物が置かれた場合、流体力により構造物が振動し周囲の流れに影響を及ぼす自励振動が発生することがあります。
このような現象は、一般に、構造流体連成問題と呼ばれます。
この場合、構造物の振動を支配する運動方程式と振動を考慮に入れたNavier-Stokes方程式が連立して解析されます。
一方、構造物が外部から強制的に加えられる力により振動する強制振動の場合は、流れ場は振動を考慮したNavier-Stokes方程式から求められます。
OverSet法
OverSet法は、主格子と副格子の間で相互的に物理量補間を行っています。
補間方法としては、補間される点の周りの3点を使用する線形内挿を使用しています。
この手法を使用すると流体中または電界を大きく移動するような弾性体の運動シミュレーションを可能とします。
構造-流体-静電場連成解析
最近では、シリコン基盤などにセンサ、回路、アクチュエータあるいは微細構造体のような様々な要素を集積化した高度な働きをする小型システムを開発することが盛んになっており、たとえば、加速度センサ、圧力センサ、静電モータ、光スイッチ、バイオチップなどがあります。
これらのアプリケーションに対して、AMPSを使用することにより、高精度な構造-静電場-流体連成解析を行うことができます。
静電モーターシミュレーション
静電モータの歴史は意外に古く,18世紀から19世紀にかけて,様々な種類の静電モータが考案されています。
しかしながら、それらのモータは力が小さかった上に,駆動に高電圧が必要であったことから,実用化されることはありませんでした。
しかし,1980年代後半より半導体製造プロセスを用いたマイクロマシンが盛んに試作されるようになると,その駆動源として大きさ0.1mm程度のマイクロ静電モータが注目を集め,様々な形態のマイクロ静電モータが試作されるようになっています。
特長としては、
- 平面的な構造により製作可能なため,半導体製造プロセスの適用が容易である。
- 電磁モータにおいては,単位体積あたりの発生力(力密度)が,寸法によらず一定であると見積もられるのに対し,静電モータの場合は,モータ寸法を微細化するほど,力密度が向上する。
などが考えられます。
参考文献 東京大学先端メカトロニクス研究室
ここでは、電磁モータとは異なる原理に基づき駆動される静電アクチュエータに着目して、AMPSの連成解析機能の一つであるOverSet法を使用した静電モータシミュレーションをご紹介します。
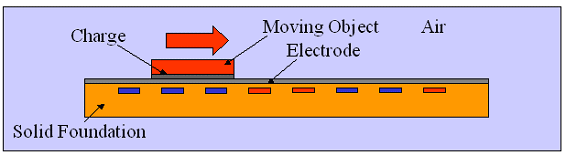
(静電モータシミュレーション)
この静電モータのメカニズムは、移動子に与えられた電荷と基盤に整列している電極に電圧を印加された電極間の静電力により移動子が駆動します。
この静電モータシミュレーションでは、移動子を取り巻く空気の流れ(空気の粘性抵抗)と電界を同時に考慮しています。
また、流体の計算には、Navier-Stokesの方程式を解いており、移動子の抗力を厳密に計算しています。
AMPSを使用することにより、位置制御シミュレーションの精度を向上させることができます。
下図は、電圧を変化させて場合の移動子の応答特性の違いを示しています。
電圧が高いほど目的とする位置に早く移動させることができることがわかります。
下図(左)は、60[V]を印加した場合の移動子のアニメーションを示しています。
また、下図(右)は、移動子の運動により、微小に電位ポテンシャルが変化している様子を示しています。
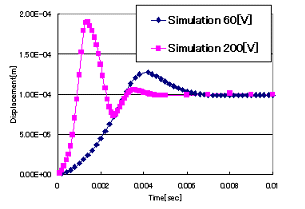
(電圧による移動子の応答特性の違い)
解析事例
- マイクロミラー
- 静電モータ
- 熱アクチュエータ
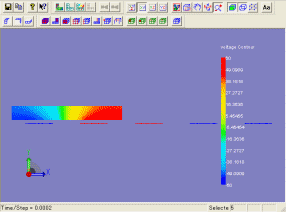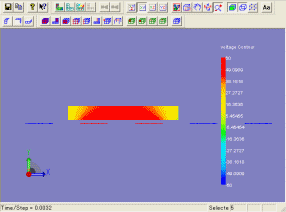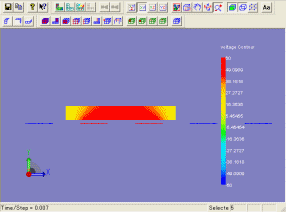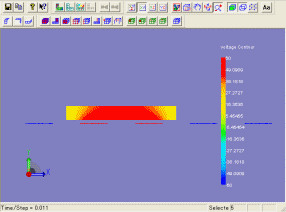
(移動子の応答アニメーション)
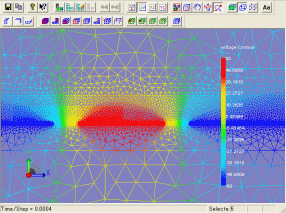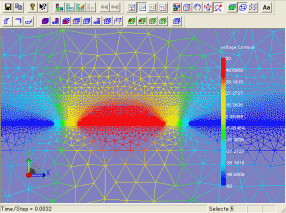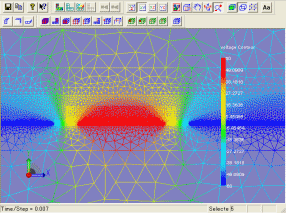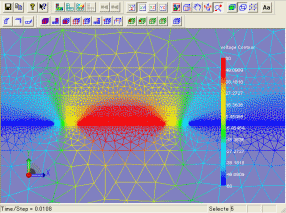
(電位ポテンシャル分布)
マイクロミラーの角度応答シミュレーション
半導体マシニング技術では、たくさんのデバイスをアレイ化したり、微細な構造を反復して、多数並べたりすることが容易にできます。
特に、静電マイクロアクチュエータは、構造が簡単であり、消費電力が少ないので、大規模のアレイ化に最適となっています。
デジタルマイクロミラーデバイスと呼ばれる投射ディスプレイ用マイクロマシンでは、画素数に対応する何百万ものの微小稼動ミラーをビデオRAMの上に作り、ミラーの傾きを静電アクチュエータで高速に変えて反射光を制御しています。
このようなことから、製品開発において、ミラー角度の精度を高めることは重要となります。
ここでは、AMPSの連成解析機能の一つであるALE法を使用したマイクロミラー角度応答シミュレーションをご紹介します。
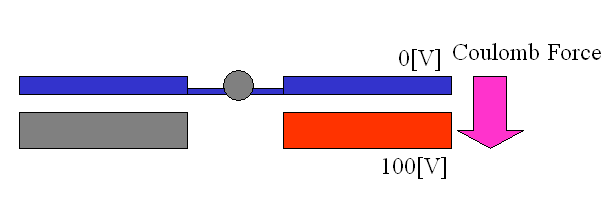
(マイクロミラーのメカニズム)
上図に示す下部の電極板に電圧印加すると、上部のミラー板と下部の電極板間にクーロン力が発生し、クーロン力を受けたミラー板は、構造変形をおこし、傾きを生じることになります。
AMPSでは、電極板間の空気の電界とミラー板の構造変形を同時にシミュレーションしています。
解析事例
- 熱アクチュエータ
その他の解析機能
アデプティブ解析法
設計や現象の解明において、より複雑な解析形状に対して、より精度の高い結果が得られるように解析することが要求されています。
有限要素法では、要素サイズを小さくすることで解を正解に近づけることができます。
しかしながら、望む精度を得るために、解析形状全体を一様に細かく要素分割すると、たちまち取り扱う解析モデルは巨大なものになってしまいます。
そこで、物理量の分布をあらかじめ予想して、物理量変化の激しい部分のみを細かく要素分割するといった効率的な要素分割が望まれます。
実際には、構造解析の分野においては、応力が高い部分や変形が大きい部分をあらかじめ要素して、そこを分割するという方法がとられます
従来では、この作業を行うのは、専門分野、有限要素法に明るく、十分な製品知識があり、過去の解析例に通じた解析者と言われる人々が、経験により応力集中などを予測して、要素分割を行ってきました。
しかしながら、解析者の経験に頼るのは、限度があり、解析形状がより複雑なものに対して効率的な要素分割を行うのは困難になります。
このようなことから、AMPSでは、効率的な要素分割を自動化するために、事後誤差評価に基づくアダプディブhp法機能を搭載しています。
この手法は、有限要素解から誤差の指標である誤差ノルムを事後推定して、その結果から要素の適応化を自動的に行います。
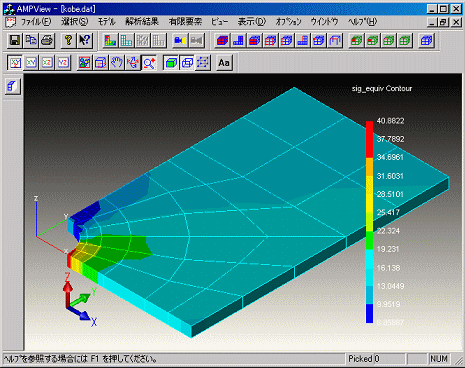
(初期メッシュ)
上図は、初期メッシュに対する応力分布となります。
ここで、プログラムは、誤差分布に基づいて、自動的にリメッシングを行います。
下図は、誤差分布に基づいて、リメッシングを行った応力分布となります。
この機能を使用することで、はじめてCAEツールを使用するユーザでも精度の高い解を求めることができます。
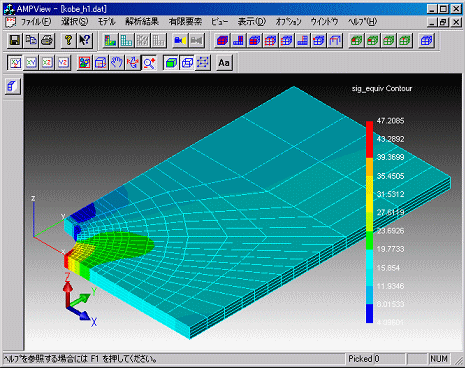
(アダプティブリメッシング)
メッシュ/結果処理
6面体メッシュ生成機能
AMPSでは、ボクセル法と押し出し法による6面体要素生成機能を搭載しています。
一般的に、6面体要素は、4面体要素よりも精度が高く、収束性も早いので、非線形解析や連成解析を行う場合は、非常に有効な要素になります。
AMPSは、6面体要素を生成するために、完全自動6面体要素生成機能と手動6面体要素生成機能を搭載していますので、フレキシブルなメッシュを生成することができます。
また、4面体要素から6面体要素を生成することもできます。
AMPSのボクセル法による6面体メッシュ生成機能は、分割数を指定するかボクセル1辺あたりの長さを指定することにより生成できます。
3DCADから取り込んでからすぐにメッシュ生成を行えるのがボクセル法の一つの特長と言えます。
下図 は、ボクセルの1辺の長さを指定してボクセルを生成した状態を示しています。
それから、CAD形状の稜線、頂点、面にボクセルの節点を投影してCAD形状にフィットさせます。
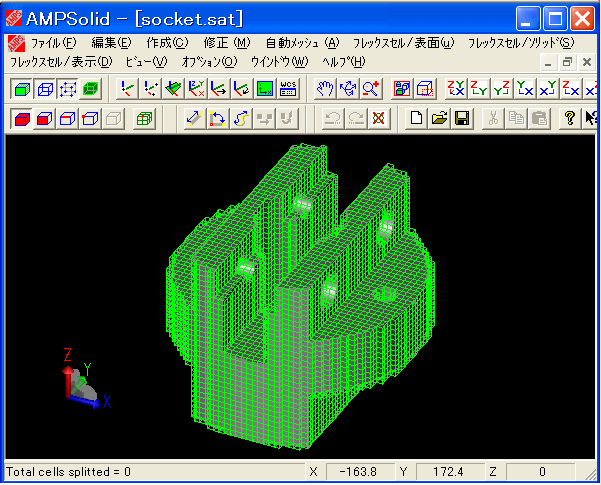
(ボクセル生成)
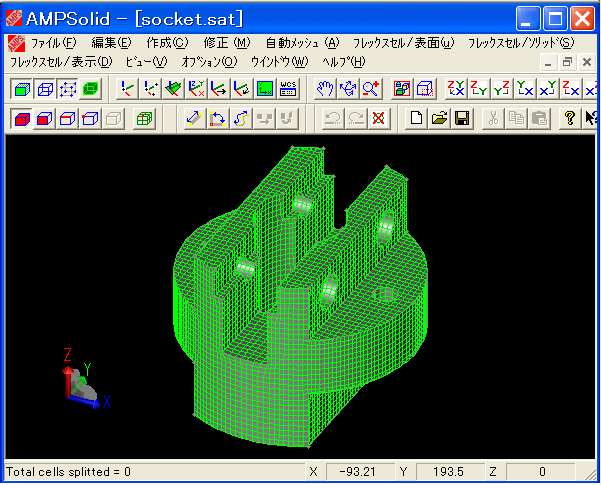
(6面体要素生成)
わかり易いユーザインターフェース
AMPSのユーザインターフェースは、使用頻度の少ないユーザでも直感的に使用できるように設計されています。
システムのメニューは、すべて日本語となっています。
また、ボタン一つで複数の物理場の連成解析(マトリクス連成、シーケンシャル連成)の設定が可能となっています。
他社のシステムと違い、少ない手続きで連成解析を実行することができます。
また、チェックボタン一つでALE法を使用することもでき、簡単に移動境界問題の設定を実施することができます。
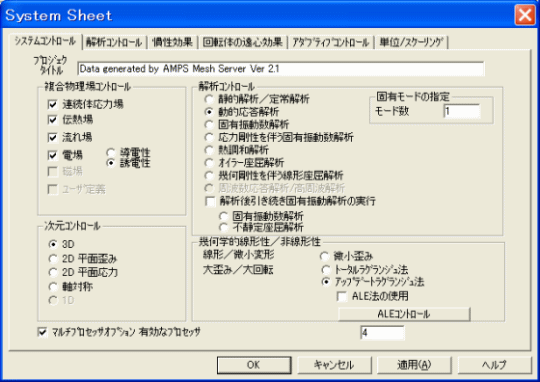
(システムコントロールページ)
結果処理
AMPSでは、結果評価に欠かせない基本的な機能の他に可視化ツールとしてアニメーション表示機能まで豊富に搭載しています。
ストリームライン図、コンター図、ベクトル図、変形図、グラフ図、梁要素に対する結果値のダイアグラム図、物理結果に対する積分機能などを揃えています。



